Je sauberer das Signal, desto besser der Klang – diese Maxime gilt seit den Gründerzeiten der High Fidelity. Doch wie “rein” muss ein Musiksignal wirklich sein, soll es “echt” klingen? Soll es überhaupt “rein” sein, fragt man sich angesichts der meist eher mäßigen Messwerte von als besonders gut klingend geltenden Röhrenverstärkern. Wir bei LowBeats meinen, es ist Zeit, den Mythos vom reinen Klang zu verabschieden: Urteilen Sie selbst – die Hörbeispiele in diesem Beitrag zeigen Ihnen, ob und wie Verzerrungen den Klang prägen.
Damit Sie auf Anhieb im Bilde sind, worum es in diesem Beitrag geht, gleich zu Beginn ein kleiner Hörversuch: In den beiden folgenden Audio-Files (Achtung, die Signale sind recht laut – Laptop-User verwenden für besseren Klang vorzugsweise einen Kopfhörer) hören Sie jeweils den gleichen, einzelnen 1.000-Hertz-Ton bei identischer Lautstärke – aber dennoch unterscheiden sich die Tracks:
Track 1:
Track 2:
Offensichtlich wird der Ton in Track 2 von leiseren “Mitspielern” begleitet, die sich als feines Sirren bemerkbar machen und den eigentlichen Ton etwas kantiger klingen lassen. Eben bei diesen “Nebentönen” spricht man von Verzerrungen. Genauer gesagt, von nichtlinearen Verzerrungen – denn neben diesen gibt es auch lineare Verzerrungen, wie sie beispielweise Klangregler oder auch die Schneidkennlinien-Korrektur im Phonoteil des Verstärkers gewollt herbeiführen. Von diesen soll jedoch hier nicht die Rede sein.
Nichtlineare Verzerrungen hingegen sind (in der Regel) ungewollt. Sie entstehen, weil Baugruppen oder -elemente im Signalweg keine idealen Eigenschaften besitzen. Besonders wichtig in diesem Zusammenhang ist, dass ihr Übertragungsverhalten, sprich ihre Eingangs-/Ausgangskennlinien nicht linear verlaufen, sondern mehr oder weniger starke Verformungen (Krümmungen) aufweisen. Somit wird das Originalsignal beim Durchlaufen mehr oder weniger stark verändert. Dadurch entstehen neben der eigentlichen Grundschwingung zusätzliche Nebenschwingungen, deren Amplitude und spektrale Verteilung vom Grad der Verformung abhängt. Der genaue Zusammenhang lässt sich dabei mathematisch klar darstellen (für spontan Wissensdurstige: http://www.sengpielaudio.com/Rechner-klirr.htm). Das ist sehr nützlich, aktuell aber nur von untergeordnetem Interesse, stehen doch In diesem Beitrag die gehörmäßig erfassbaren Auswirkungen von nichtlinearen Verzerrungen im Blickpunkt.
Die Mär vom reinen Klang: Stichwort Klirrfaktor
Es liegt nahe, dass Audio-Entwickler seit jeher versuchen, nichtlineare Verzerrungen durch konstruktive Maßnahmen so gut wie möglich zu vermeiden. Zur Blütezeit der High Fidelity Mitte der 70er Jahre des letzten Jahrhunderts brach sogar ein regelrechter Wettstreit unter den Herstellern aus, extrem geringe Verzerrungswerte mit möglichst vielen Nullen nach dem Komma zu erreichen.
Natürlich stellt sich da zunächst mal die Frage, welches Maß an nichtlinearen Verzerrungen überhaupt hörbar ist – keine eindeutige Angelegenheit, wie wir noch erfahren werden. Eine eher pragmatische Antwort darauf gab die einstige deutsche Hi-Fi-Norm, die altehrwürdige DIN 45500: Sie sah für Verstärker bei der geforderten Mindest-Nennleistung von 6 Watt pro Kanal einen Klirrfaktor von maximal einem Prozent vor.
Stichwort Klirrfaktor: Der prozentuale Anteil nichtlinearer Verzerrungen in einem Audiosignal wird umgangssprachlich zumeist als Klirrfaktor bezeichnet – häufig findet man aber auch die Angabe “Total Harmonic Distortion” (THD). Grundsätzlich meinen Klirrfaktor und THD das Gleiche, auch wenn ihre jeweilige Bestimmung geringfügige Unterschiede aufweist.
Ein Prozent Klirrfaktor – kann man das überhaupt hören? Und wenn ja, wie hört sich das an? Auch das hat LowBeats für Sie simuliert: Spielen Sie dazu die beiden folgenden Audio-Files ab – in Track 4 haben wir zum ursprünglich reinen Ton nichtlineare Verzerrungen von genau einem Prozent hinzugefügt.
Track 3: 1.000 Hz -6dBFS, unverzerrt
Track 4: 1.000 Hz -6dBFS, 1% Klirrfaktor
Das Ergebnis ist eindeutig: Klirrfaktoren in der Größenordnung von einem Prozent sind gehörmäßig leicht wahrnehmbar – zunächst mal allerdings im direkten Vergleich mit hochreinen, sinusförmigen Tonsignalen. Aber gilt das auch bei komplexen Signalen wie beispielsweise Musik?
Die Mär vom reinen Klang: Verzerrungen sichtbar gemacht
Bevor wir uns dieser Frage widmen, hier noch ein weiterer kurzer Hörvergleich:
Track 5:
Track 6:
Hoppla, hier wird’s schon schwieriger, zwischen unverzerrtem (Track 6) und verzerrtem Signal (Track 5) zu unterscheiden – obwohl dieses ebenso wie Track 4 einen Klirrfaktor von genau einem Prozent aufweist. Es scheint also gehörmäßig auffällige und weniger auffällige Verzerrungskomponenten vom reinen Klang zu geben.
Um dieses Phänomen aufzuklären, ist ein Sichtbarmachen der Verzerrungskomponenten per Diagramm sehr hilfreich. Besonders anschaulich dokumentiert das die spektrale Darstellung in der Frequenzebene – genau das Richtige also für unseren Labor-Analyzer.
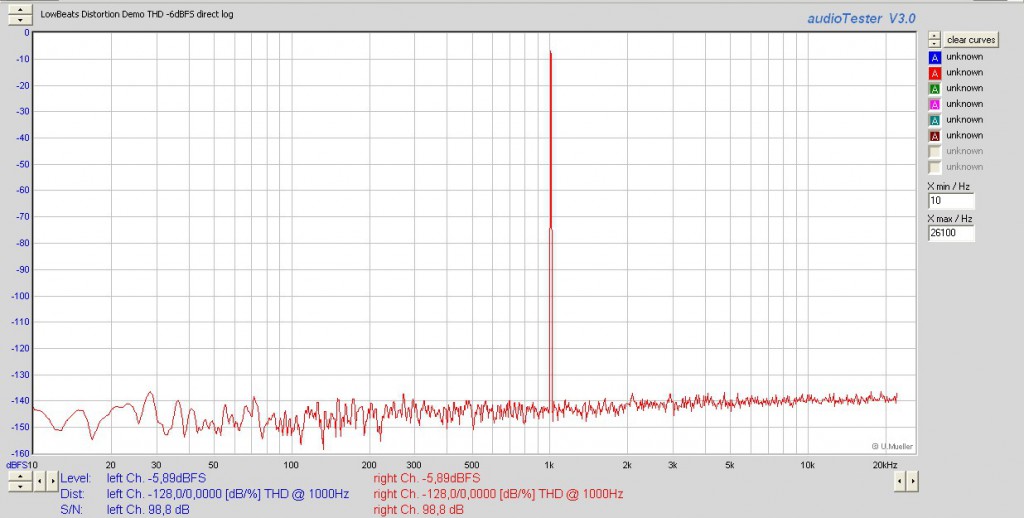
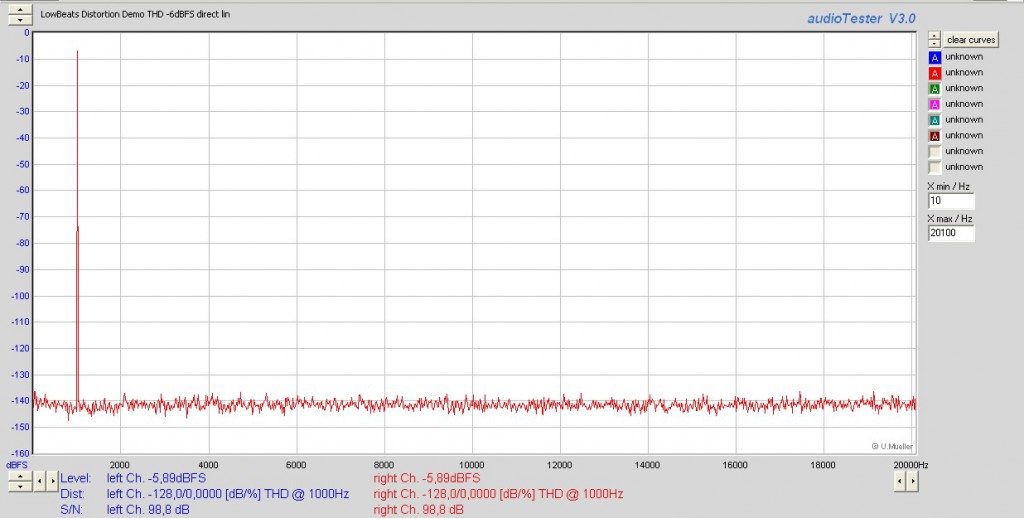
Die beiden obenstehenden Diagramme zeigen dabei das unverzerrte Signal aus Hörbeispiel 1 in jeweils unterschiedlicher Darstellungsweise – hier erkennt man lediglich eine steile “Nadel” (was einem einzigen Ton entspricht) bei exakt 1.000 Hertz, die aus dem in der Praxis vernachlässigbaren Rauschgrund herausragt. Die Verzerrungswerte vom reinen Klang, so überhaupt vorhanden, liegen also deutlich unterhalb der Messgrenze unseres Analyzers.
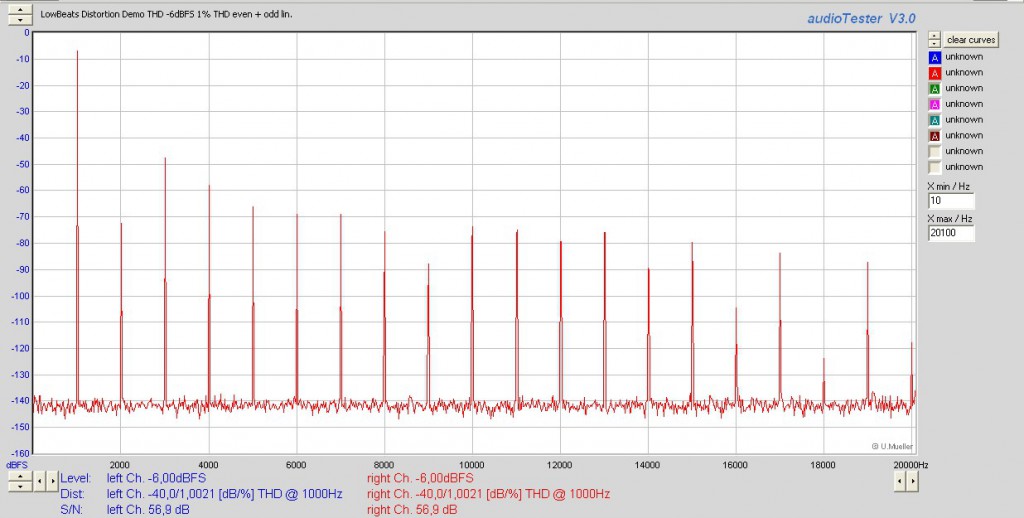
Anders dagegen in Diagramm 2: Zu dem 1.000-Hertz-Ton haben sich hier noch weitere, kleinere (und damit leisere) Nadeln bei anderen Frequenzen hinzugesellt. Auffallend dabei ist, dass sich diese allesamt oberhalb vom 1.000-Hertz-Signal und zudem in regelmäßigem Abstand zueinander befinden. Die Frequenzskala am unteren Bildrand zeigt darüber hinaus, dass sich diese Nebentöne stets bei ganzzahligen Vielfachen der Grundfrequenz von 1.000 Hertz einstellen. Aufgrund ihres stets ganzzahligen Verhältnisses bezeichnet man den Grundton und die durch Verzerrungen bedingten Obertöne als “Harmonische”: Der 1.000-Hertz-Grundton bildet dabei die 1. Harmonische; die 2. Harmonische liegt dann eine Oktave höher bei 2.000 Hertz, gefolgt von der 3. Harmonischen bei 3.000 Hertz sowie der 4. Harmonischen bei 4.000 Hertz usw. – so erklärt sich auch der Begriff „Total Harmonic Distortion“.
Geradzahlige und ungeradzahlige Verzerrungen
Die spektrale Verteilung der harmonischen Verzerrungsprodukte hängt dabei unmittelbar mit ihrer Entstehungsursache zusammen – der bereits erwähnten Verformung von Übertragungskennlinen. Diese fallen bei den verschiedenen Gerätetypen erwartungsgemäß recht unterschiedlich aus. Sie sind darüber hinaus auch noch abhängig vom Grad der Aussteuerung – je höher die Lautstärke, desto größer in der Regel der Anteil der Verzerrungen und die Entfernung vom reinen Klang. Das bedeutet in der Praxis, dass man je nach Gerätegattung mehr oder weniger typische Verzerrungsprofile feststellen kann. So dominieren mal die geradzahligen Harmonischen und mal die ungeradzahligen, wobei durchaus auch mal Fehlende auftreten können.
Vor diesem Hintergrund wenden wir uns nun noch mal kurz den Hörbeispielen 4 und 5 zu – dem Vergleich mit deutlichen sowie kaum hörbaren Verzerrungskomponenten bei gleichem Klirrfaktorwert von einem Prozent. Die Unterschiede zwischen beiden Files zeigen die beiden folgenden Diagramme:
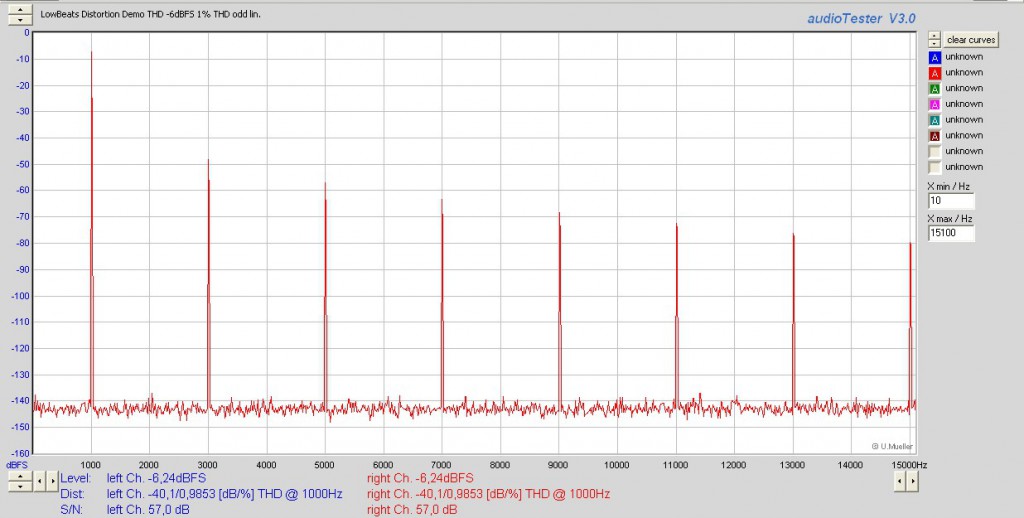
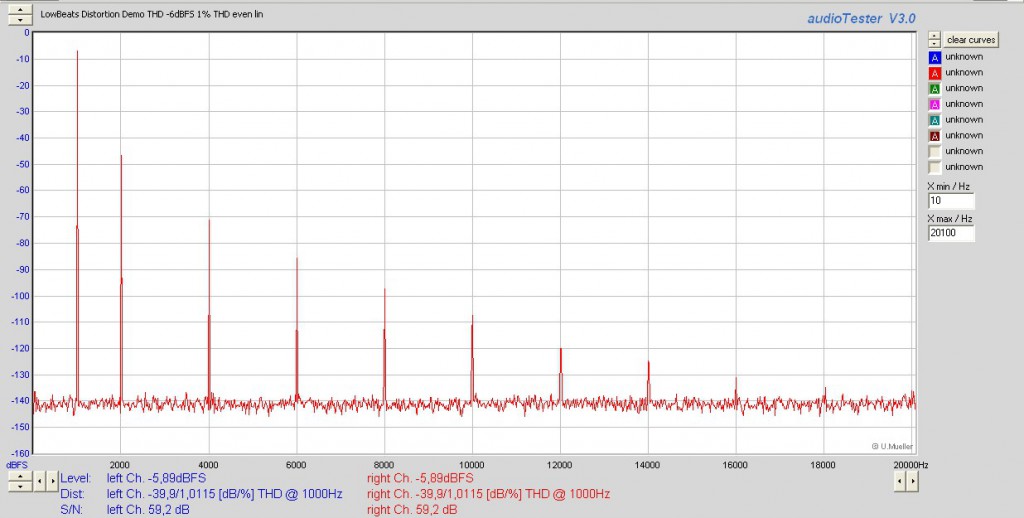
Während im oberen Diagramm zu Track 4 neben dem Grundton ausschließlich ungeradzahlige Harmonische vertreten sind, weist das untere Diagramm zu Track 5 ausschließlich geradzahlige Harmonische aus. Hier liegt auch des Rätsels Lösung: Ungeradzahlige Harmonische fallen bei gleichem Gesamtbetrag gehörmäßig stärker auf als geradzahlige, weil sie weniger angenehm klingende musikalische Intervalle zum Grundton bilden. Für einen unmittelbaren Hörvergleich haben wir in den beiden folgenden Hörbeispielen den 1.000-Hertz-Grundton komplett entfernt, so dass Sie ausschließlich die Verzerrungsanteile hören können – in Track 7 die ungeraden, in 8 die geraden. Damit Sie den Lautstärkesteller nicht voll aufdrehen müssen, haben wir den Signalpegel beider Files um 20 Dezibel angehoben. Dadurch hören Sie die Verzerrungsanteile viermal lauter als in den Original-Files mit 1.000-Hertz-Ton.
Track 7: Ungeradzahlige Klirranteile ohne Grundton
Track 8: Geradzahlige Klirranteile ohne Grundton
Interessant in diesem Zusammenhang ist natürlich, welche Verzerrungsanteile für die unterschiedlichen Audiokomponenten charakteristisch sind. Grundsätzlich gilt folgender Zusammenhang: Symmetrisch verformte Kennlinien erzeugen vorwiegend ungeradzahlige Harmonische, unsymmetrisch verformte hingegen vorwiegend geradzahlige Harmonische. In der Praxis heißt das beispielsweise: Röhrenverstärker im Eintakt-A-Triodenbetrieb produzieren vorwiegend geradzahlige, während Transistorverstärker, analoge Bandmaschinen und auch Lautsprecher vorwiegend ungeradzahlige Harmonische erzeugen. Solche generalistischen Aussagen gelten allerdings nur in erster Annäherung, denn aufgrund der zahlreichen Einflüsse fallen die Verzerrungsspektren nur selten wirklich reinrassig aus. Zudem können erfahrene Audioentwickler das Verzerrungsverhalten und damit den Klangcharakter ihrer Schaltungen durchaus in die gewünschte Richtung lenken – und die ist meist weit weg vom reinen Klang, wie oft er auch angepriesen wird.
Fazit: Verzerrungen prägen den Klang
Und genau das können Sie nun mit Hilfe der folgenden Musikbeispiele nachvollziehen, die wir mit typischen, realistischen Verzerrungsspektren gezielt angereichert haben. Verzerrungen vom reinen Klang sind der prägende Faktor der akustischen Wahrnehmung. Gönnen Sie sich doch einfach mal den Spaß und versuchen zunächst durch Hören herauszufinden, welche der beiden folgenden Aufnahmen einer akustischen Gitarre das Original und welche die bearbeitete Version ist. Tipp: Achten Sie nicht nur auf den Attack, sondern auch auf den Ausschwingvorgang der Saiten – die richtige Lösung erfahren Sie am Ende des Textes.
Akustik-Gitarre Track A:
Akustik-Gitarre Track B:
Wie Sie an diesem Musikbeispiel feststellen können, fällt es leichter, sich für eine angenehm klingendere Version zu entscheiden als sie einwandfrei dem Original oder der Bearbeitung zuzuordnen. Ebenso spannend ist auch die Tatsache, dass verschiedene Instrumente recht individuell auf unterschiedliche harmonische Verzerrungen ansprechen. Diese müssen dem Klangcharakter keineswegs immer abträglich sein, sondern können ihn sogar unterstützen. Falls Ihnen also demnächst wieder jemand während einer gelungenen Musik-Vorführung vom reinen Klang der Anlage schwärmt, so schenken Sie ihm ein Lächeln und denken sich: “Klingt schöner als echt.” ;-)
… noch ein paar Tipps:
Um Ihnen möglichst authentische Hörbeispiele an die Hand zu geben, haben wir harmonische Verzerrungen vom reinen Klang nur in praxisnahen Größenordnungen hinzu generiert. Daher fallen die klanglichen Unterschiede eher subtil aus – eben so, wie es auch beim Anhören unterschiedlicher HiFi-Komponenten der Fall wäre. Wir empfehlen deshalb, beim Anhören der Beispiele qualitativ gute Lautsprecher, besser noch Kopfhörer zu verwenden. da diese selbst von Haus aus relativ geringe Verzerrungen erzeugen. Beachten Sie bitte, dass die maximal erzielbare Tonqualität prinzipbedingt auch von der Übertragungsrate Ihrer-Internet-Verbindung abhängt. Ehrensache, dass wir für die Hörbeispiele keinerlei Klangregler oder Kompressoren eingesetzt haben: Die Klangunterschiede beruhen ausschließlich auf unterschiedlichen Verzerrungsspektren. Zum Schluss noch die Lösung des Hör-Vergleichs mit der akustischen Gitarre: Track A ist das Original.
Ähnliches Thema:
Jitter entmystifiziert
Empfehlenswerter Beitrag zum Thema Klirrfaktor:
sengpielaudio.com/Rechner-klirr